Question 1
We are given as input a set of 







Question 2
We are given as input a set of 


























Question 3
Consider an undirected graph 











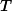















Question 4
Suppose 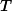










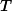

Question 5
Consider an undirected graph 











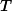








No comments:
Post a Comment